表計算Excelを利用した流体計算

Excelなどに代表される表計算は、技術分野でも幅広く活用されており、流体計算もその対象である。
流体力学における表計算の活用は多岐にわたるが、これは表計算の機能が著しく高まってきたことに関連している。流体力学の支配方程式は、ラプラス方程式やナビエ・ストークス方程式などの偏微分方程式が代表的なものである。例えば、物体周りのポテンシャル流は、ラプラス方程式の差分形を利用して、図1のように計算できる。

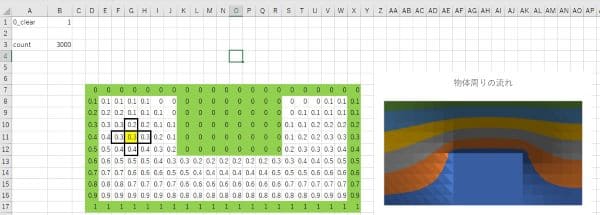
図1. 物体周りのポテンシャル流

表計算のシートは二次元の物理平面と見なすことができて、各セルは計算格子に対応する。図1で緑色の部分は計算領域の境界を表しており、境界条件の値が予め書き込まれている。緑色の境界に囲まれた領域の各セルには、ポテンシャル流の支配方程式である、ラプラスの方程式が記入されている。一つのセルが記入されると、それをコピーすることによって計算領域が完成する。例えば、図1の黄色に着色されたセルには、上下左右のセルの平均になる式が記入されている。以上のように計算準備ができると、表計算の繰り返し計算機能をオンにして、値が収束するまで計算を続行する。その後、図1の計算領域を選択して、等高線を表示させると、図1右側のように流れの様子を図示できる。図1は、流線を表しているが、機械工学の場合は温度分布、電気工学の場合は電位あるいは電流の様子を表している。従来、このような問題を解く場合は、コードを書いて繰り返し計算を行うのが通常であったが、この例のように表計算を利用すると、かなり容易に計算結果を得ることができる。
図1のような数値計算は、理論値や実験値と比較することにより、その有効性を確かめることができる。図2は、図1と同様に拡大管のポテンシャル流をラプラスの式を用いて表計算で解いた流線と圧力分布を表している。このような流れには図3のように理論解が知られており、簡易計算にもかかわらず、表計算の解が極めて正確であることが分かる。

（a）流線

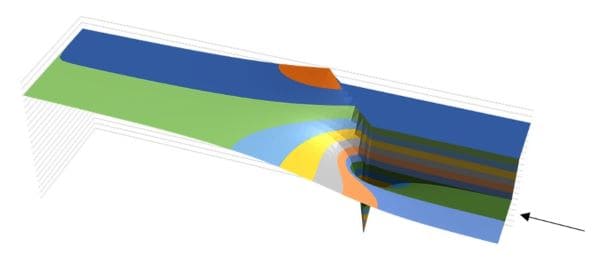
（b）圧力分布

図2. 拡大管流れ（ラプラス方程式表計算）

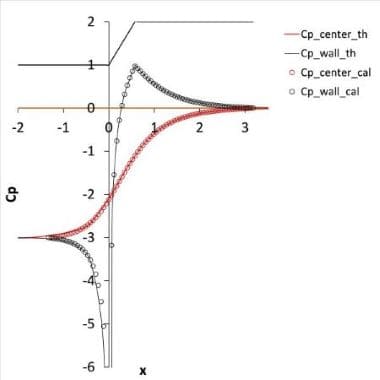
図3. 拡大管圧力分布（理論値と表計算値の比較）

（a）音速分布

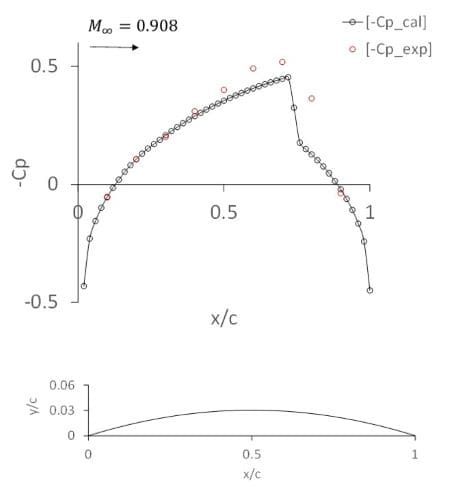
（b）翼面圧力分布

図4. 6％放物翼周りの遷音速流　M∞=0.908

ラプラス方程式と同様に、圧縮性流れの完全ポテンシャル方程式を用いて、表計算で図4のような6％翼厚の放物翼周りの遷音速流れを解くことができる。図4（a）は音速分布であり、（b）は翼面の圧力分布である。衝撃波を捉えることができ、衝撃波前方は膨張領域（0.19≤x/c≤0.78）で超音速流になっている。翼面の衝撃波は巡航中のジェット旅客機の窓から日差しの向きのよっては観測できることがある。

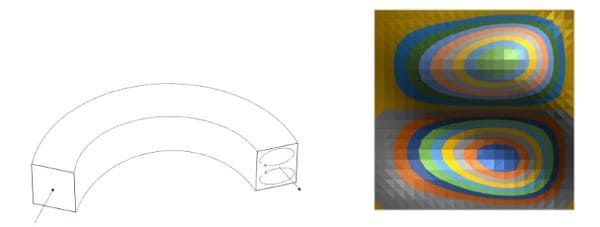
図5. 矩形断面曲がり管二次流れ

図6. 矩形断面曲がり管　速度分布

表計算では、ラプラス方程式と同じ要領で、ナビエ・ストークス方程式も解くことができる。図5は、レイノルズ数Reが100の十分発達した矩形断面の曲がり管内の二次流れを表している。管の曲がりによって、管断面内に二次流れが生じる。また、図6のように主流は、遠心力のために外周側に偏った分布となる。
工学上便利な表計算の機能の一つとして、逆行列演算が挙げられる。航空工学の分野では翼周りの計算にパネル法が用いられる。この計算法は、翼面にラプラス方程式の解である渦点などを配置して、流れが翼面に沿う条件から渦点などの強さを決めようとするもので、連立一次方程式の解として求められる。

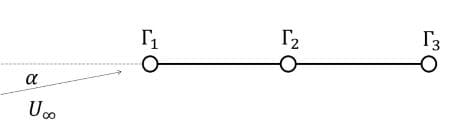
図7. 渦点で近似された平板翼

基本的な例として、図7の離散渦で近似された平板を考えてみよう。図7の平板において、所定の位置において流れが平板に沿う条件と、後縁で流れが滑らかに流れさる条件から、渦点の強さΓi（i=1,2,3）に関する連立一次方程式が得られる。これを表計算のMINVERSE機能により逆行列を求め、右辺に掛け合わせて渦点の強さΓi（i=1,2,3）が得られる。
図8は、Garrick-片柳による、同心円管内流れを等角写像によって求めた、隙間フラップの理論解と、図7で示される方法を線形分布に発展させたパネル法の数値解を比較したものであり、パネル法が有効であることが分かる。図9はNACA2414複葉翼の結果である。これらは、二重連結領域の流れと呼ばれる。

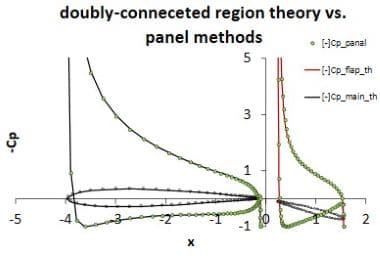
図8. 迎角10°における隙間フラップの圧力分布

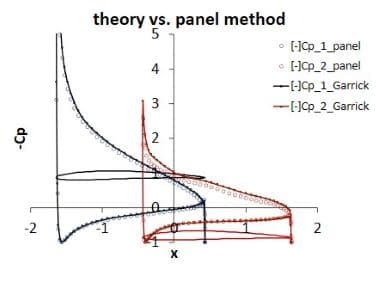
図9. 迎角10°におけるNACA 2412複葉翼圧力分布

近年多重連結領域のポテンシャル流の問題を鏡像法で解析的に求められることがCrowdyによって示されている。図10はMathemaiticaを利用した3重連結問題である循環の無い3円柱の解析解の例である。通常は数値解によって求められる性質の問題である。
図11は、二重連結領域の場合で循環を有する場合のCrowdy法による鏡像解の例である。この解は、図8の解に対応したもので、図11中の赤丸は翼の前後縁、黒丸は淀み点を表している。図12は、表計算で求めたパネル法の数値解の速度との比較であり、両者はよく対応する。

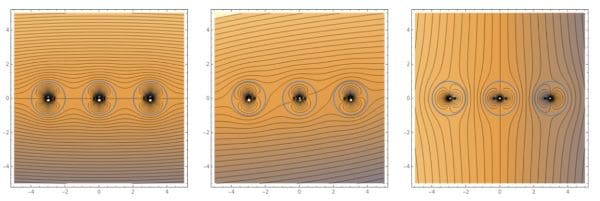
図10. Crowdy法による迎角が変化する3円柱まわりのポテンシャル流解析解

図11. Crowdy法による循環を有する2円柱周りのポテンシャル流

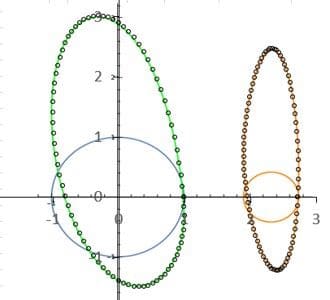
図12. パネル法とCrowdy法の円柱表面速度分布比較（図11参照）

翼周りの流れの計算において、パネル法は有効であるが、後縁が極めて薄いような場合には、係数行列の値が0になり、逆行列の計算が困難となる。これは、例えば後縁近傍の相対する上下面の二つの選点における境界条件が同じ式になってしまうことに由来している。このような場合には、図13に示すように、単位円柱まわりの流れをシュワルツ・クリストッフェル変換によって、多角形近似した任意翼型に写像する方法が有効である。図14には、この手法によって計算された、S1223翼の1％ガーニーフラップの効果が示されている。

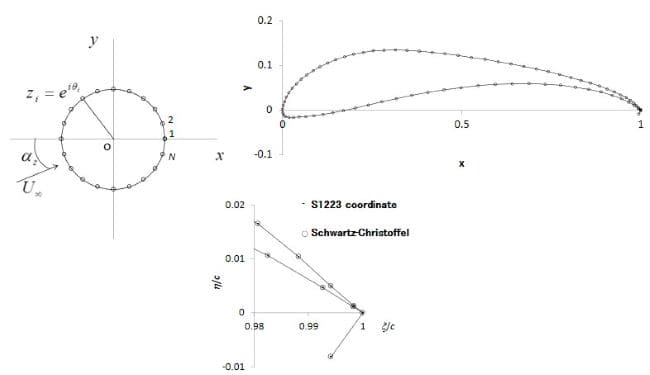
図13.単位円のS1223翼型へのシュワルツ･クリストッフェル変換（1%ガーニーフラップ付）

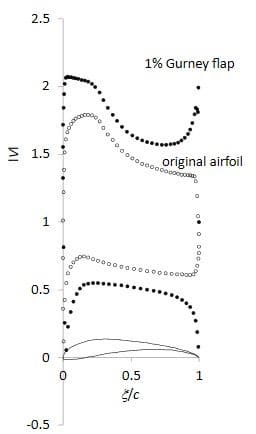
図14. S1223翼型における１％ガーニーフラップの効果

衝撃管問題には解析解があって、数値計算結果の検証に利用されている。この問題を航空機事故の問題に当てはめることができる。図15は、航空機圧力隔壁破損時の状態を胴体断面積が一定の衝撃波管であると模擬した場合の圧力変化などを表している。
（a）は、航空機の高度7285mにおける客室圧力と外気圧を表しており、公式記録に従うとその比は2.52 である。（b）は、隔壁破損直後、機体後部に向かう波面速度383m/sマッハ数1.23の右向き衝撃波と、客室内を左向きに進行する左端速度343m/sの膨張波を表している。（c）は、機体尾部からの速度　296m/sの左向き反射衝撃波を表している。実際の機体では、機体尾部は円錐状に断面積が減少しているため、最初の客室圧力に近い、反射衝撃波の圧力は（c）の場合より高くなることが、図13の数値計算や浅底水槽の簡易実験で確かめることができる。
実際の航空機では、このような機体尾部における急激な圧力上昇により構造的な損傷が生じたとされている。また、客室の圧力は突如半減し、温度も零下となる。温度や密度には、客室空気の流出面と押される側の外気面との境界である接触面に不連続が現れる。破損初期の室内空気の流出速度は、108m/sに達する。
隔壁破損から、衝撃波が機体尾部に達するまで 0.026s膨張波が客室先頭部に達するまで　0.146sであり、実質瞬間的な現象となる。

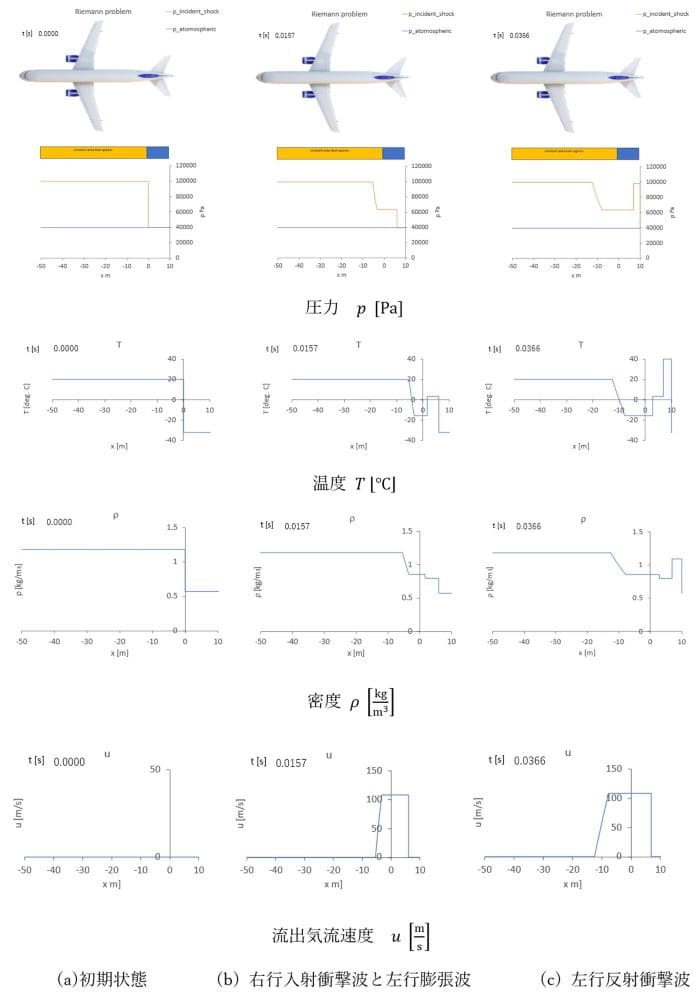
図15. 航空機隔壁破断時の衝撃波管近似

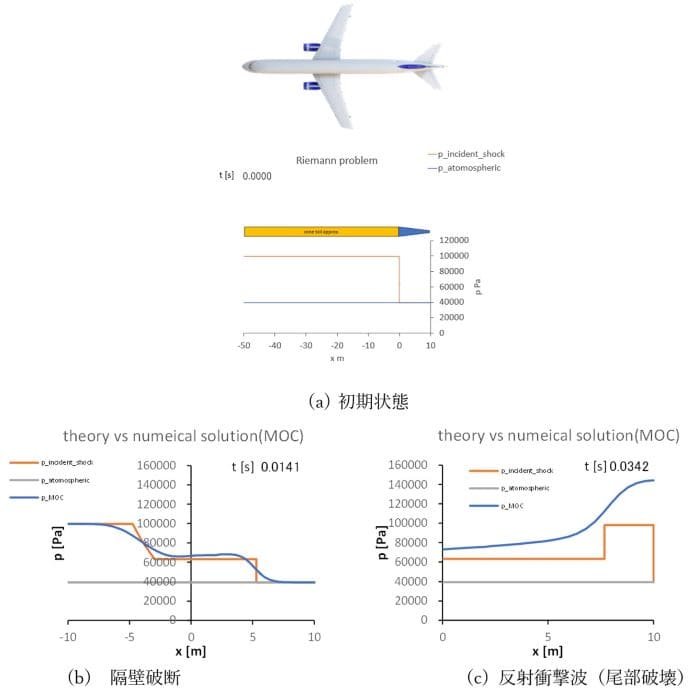
図16. 航空機圧力隔壁破断　尾部円錐形数値解（青線）と円管解析解（オレンジ）

衝撃波に関する問題では、図17のようなテイラー・マッコールによる円錐周りの錘状流の数値解が知られている。図18は、二次の項を省略した近似テイラー・マッコール方程式の石松解を表計算やMathematicaで求めたものである。本来は常微分方程式の数値解として計算され、数表などに整理されているものであるが、解析式で表現できるため、ウエーブライダーなどの設計手段として有効なものであり、手軽に解を計算できる。

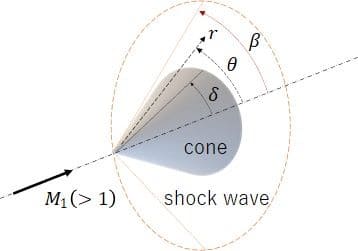
図17. 円錐周りの錘状流

図18. 石松解（M1＝5　δ＝10.48° β＝16°）

ここで紹介したように、表計算を利用すると、流体力学における解析解や数値解を容易に扱うことが可能となる。特に初めて流体計算を学ぶ場合や、設計的な活用が有用であると考えられる。

株式会社英知継承では、本テーマに関して当該専門家による技術コンサルティング（技術支援・技術協力）が可能です。下記よりお気軽にお問い合わせください。

▼「機械」に関連する技術解説一覧

スクロール圧縮機の構造と特徴

伝熱工学で扱う熱移動の３形態（熱伝達・熱伝導・ふく射伝熱）