ワイブル分布と指数分布

たいていの方は「正規分布」についてはよく見慣れた分布であろう。ヒストグラムというQC７つ道具の一つも正規分布につながり、多くの分布は正規分布に近似される。しかしながら、「ワイブル分布」や「指数分布」についてはあまりよく知られていない。「正規分布」がQCや日常データ解析でよく使われるのに対して、今回解説する「ワイブル分布」や「指数分布」は、寿命や故障形態の計算など信頼性工学の場面にてよく使われている。

1. ワイブル分布と指数分布はどのように役立つか？

ワイブル分布･指数分布は、例えば下記のようなことに応えることが可能な計算方法である。

① 使い始めに不良がどっと出たが、その後どうなっていくのか不安。
② 安定して使用中の場合には、どの程度の不具合が予測されるのか？
③ しばらく不良が出ないが、この状態はいつごろまでと期待できるのか？
④ 不良個数が使用中ゼロであっても、「10時間でゼロ」と「100時間でゼロ」の信頼度（品質の差）はどう表現できるのか？　同様に「100時間で不良ゼロ」は最大、楽観的に、どの程度までもつといってよいのか？「1000時間で不良ゼロ」ではどうか？
⑤ 劣化モードかどうかはどう判断するのか？　偶然の不良発生との識別は？

ワイブル分布・指数分布は生物の実験でも使える。以前に魚毒実験のデータ解析を手伝ったことがあるが、問題になるのは、その魚がその毒で死んだのか、元々体質的に弱かったか、病気だったのではないのか、ということの区別である。この場合でも比較対象群と比べるとき、ワイブル分布や指数分布を応用すれば数少ない魚で実験・解析することが可能となる。
一方、指数分布の「指数」は指数関数的に増加とかいう場合によく使われる言葉であるが、実は指数分布は「増加の正反対」である。信頼性工学ではワイブル分布・指数分布ともによく使われるが、ワイブル分布からはじめると理解しやすい。ワイブル分布の一つの特異点が指数分布ということになるので、ワイブル分布が理解できれば指数分布も理解でき、指数分布が重用される理由もわかるという理屈である。どうしてそうなるのかは、以下に順次説明する。

2. ワイブル分布の誕生

ワイブル分布は1939年スウエーデンのワイブルによって、材料の破壊強度の分布を表現するために考案されたものである。多くの寿命データに適合されることがわかってきて、今や信頼性の寿命解析の王道になっている。図1の最弱リンクモデルは、チェーンの一番弱いところが切れた場合、他のチェーンがいくら切れてなくても、そのチェーンの故障となり機能停止を招く。これを数式化しただけでなく、ワイブル確率紙の開発によって、今現在でも通用する故障の見える化を実現したものである。

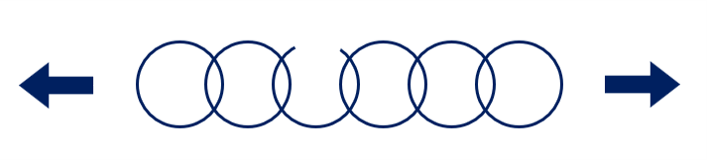
図1. 最弱リンクモデル概念図

3. ワイブル分布の基本的考え方

人間は身体のどこか一部が病気で悪くなっても、他の部分でカバーできることが多いため、このモデルには載らない。しかし半導体素子や電子部品は、デバイス内に保護回路が完備されているわけではないので、どこか一部が壊れると、素子全体の機能停止＝故障となるためこのモデルに載る。たとえば、パワートランジスタのダイボンディングに亀裂が入ると熱抵抗が高くなり、いくらエミッタやベースに問題がなくても故障に至る。

4. 故障発生時期とワイブル分布

人間は（他の生物も）生まれてから、何年か生き、最後には必ず死に至るわけである。今は状況が変わっているが、従来、とくに昔（昭和以前）の日本では、幼児の死亡率はかなり高かったようである。どの時点をもって生まれたか、とカウントするのかはよく知らないが、生まれたばかりや幼児期は病気も事故もかかる機会は多いうえに抵抗力や体力が弱く、すぐ亡くなることが多かったようである。しかし時間経過とともに急速な死亡数は急激に低下して、その後はしばらく安定した生存率で推移する。やがて寿命域に入るが、寿命域ではたいていの人が亡くなっていくから、年齢に対する死亡率は急上昇しているわけである。死亡率を部品や装置の故障率に置き換えると、図２のようになる。

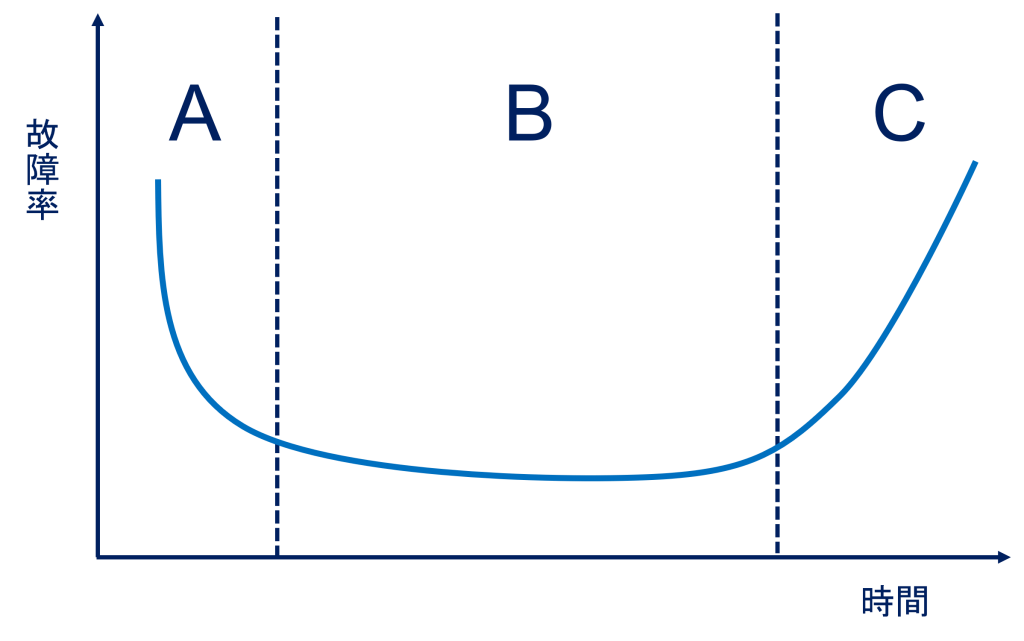
図2. 故障率と時間の経過

図2は、バスタブカーブ（バスタブ曲線）であり、ユニットバスにあるようなバスタブ断面に似ていることから、このように呼ばれている。領域Aを初期故障域、Bを偶発故障域、Cを摩耗故障域という。
例に挙げると、半導体素子などは出荷前にエージングやデバッギングを行い、初期不良を取り除く。この時点の故障や出荷後初期使用段階での故障は多く、その後急速に激減する（A領域）。使用段階に入ってある程度時間が経過すれば、大きく故障率が増加することはなく安定する（B領域）。そうは言っても、10万時間以上もたてば、寿命がきて再び急激に故障率が増大することになる（C領域）。
これを見ればわかるが、故障率のカーブは一筋縄ではいかない。領域ごとに変わっていくからである。この初期故障域も偶発故障域も摩耗故障域も共通的に説明できる関数が「ワイブル分布」である。この基本となるものが図1の最弱リンクモデルで、図２を数式化したものがワイブル分布だということになる。

5. ワイブル分布を式で表す

信頼度R(t)は時間をｔとして、次のように表現する。

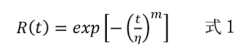
ηを特性寿命と呼ぶ。約63.2％が故障する時間である。
不信頼度F(t)は、1からR(t)を引いたものだから、次のように表される。

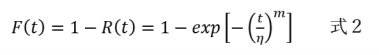
これらはワイブル分布の式であるが、通常は故障率で表現する場合が多いので、故障率で表現する。故障率はλ(t)とおいて、式2の微分であるから次のような式3となる。

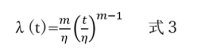
6. ワイブル分布を図で表す

故障率でみると図3のようになる。ｍによって異なる形になる。ｍは「形状パラメータ」と呼ばれ非常に重要な指標である。

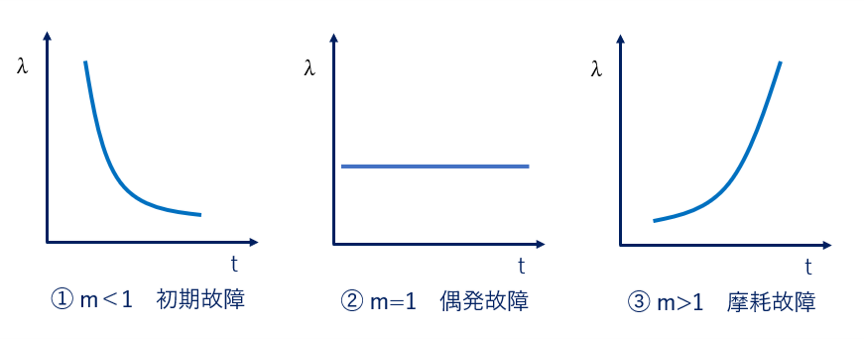
図3. ワイブル分布の図示（形状パラメータｍと故障域）

実際には、ワイブル確率紙を使って、ｍやη、平均寿命μを求める方法がお勧めである。ここで言いたいことは、ワイブル分布を使えば、ｍの大小によって全ての故障域を表現することができるということである。非常に便利な分布式である。

7. 指数分布との関係

ワイブル分布は様々なステージの故障域に使えると述べたが、特にこの分布で重要となるのは形状パラメータｍである。ｍが1前後で故障率が大きく変わるからである。実際の解析では、「故障域が初期だから、ｍが1より小さい」ということではなくて、「ｍが1より小さいから、初期故障域だ」と判断するわけである。このように、ワイブル分布を考えることによって、故障域や故障モードを判断する。
ｍ＝1の場合は、偶発故障域であるということで、この偶発故障域こそが指数分布になる。

式3にｍ＝1を入れると、λ(t)=1/ηとなって、λが一定になる。これは図3の②を表現している。分布関数は、式2より次のような式4となる。

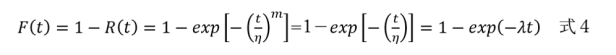
式4をｔで微分したものは密度関数であるので、それをf(t)とすれば次のように表される。

これはλが定数であるから、指数関数的に密度関数が低下することになる（図4）。
これが指数分布である。

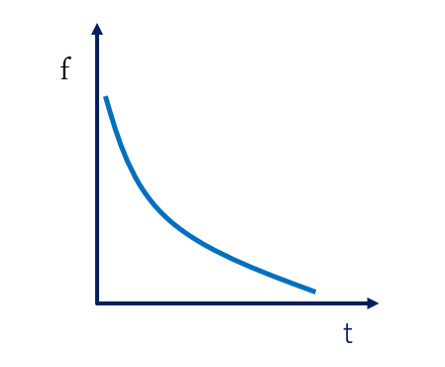
図4. m=1のときの密度関数

8. 指数分布が大事な理由

指数分布が大事な理由として結論から言えば、「3つの領域のうち、最も大事な領域の故障分布だから」である。消去法から説明すればわかりやすい。 まず初期故障は、信頼性でいう寿命の概念からすれば、名前通り「初期故障」であって、どちらかといえば品質管理の対象領域である。実際、ちょっとした配線ミスや組付け不具合、異品種混合のような品質管理上の不具合で、検査をスルーしたものが原因となるものが多いのが、この初期故障域である。半導体のパワー系なら、熱抵抗の値がセンターに入っていても、測定条件が信頼性まで考慮されていないと、ダイボンディング時に入ったボイドやクラックが、実使用段階で熱暴走によって破壊することが多いのだが、これも初期故障の例である。しかし、故障率が急速に減少していくのが、この領域の特徴である。ワイブル分布で、形状パラメータｍの値が１より小さいとこの領域であることが分かるから、品質管理上の心配はもっともだが、信頼性寿命の観点からは「故障はそのうち収まる」と思っていいのである。（もちろん、この領域でのコスト損が大きいかどうかは、別次元の話である。） 次に摩耗故障域である。これはワイブル分布で、形状パラメータｍが1より大きい、3とか4以上の場合である。これは設計的に決まってくるので、固有技術の問題となる。ここでの信頼性を上げるには、材料を変更して高信頼度部品を使うとか、機構改造しないと無理な話になる。使用条件の見直しも有効である。しかし、予測や推定の解析屋さんからすればこれは固有技術の世界だといえる。 そうすると最後に残った偶発故障域というものが、一番重要なものになる。これこそ、信頼性解析の真骨頂というわけである。なぜなら、名前通り、いつ発生するかわからないからである。そこで、その場合の寿命がどのくらいだとか、どのくらいの生き残りになるのかということが計算できるというのは大いに魅力になる。ちなみにこの偶発域の時間を耐用寿命という。耐用寿命というのは日常会話風でわかりやすいが、初期でも摩耗でもなく、その中間の偶発域のことを言う。もちろん、形状パラメータｍが1であること＝指数分布であることから、様々なケースの寿命や故障率計算が可能に（簡単に）なっている。 1項のどういうときに役立つか？で課題例として挙げた②，③，④は、この指数分布を使えば簡単に計算でき、対応策を考えることができる。そこで、②，③，④に関連したデータ解析を次に示す。ちなみに、①はワイブル分布でｍ<１となり、初期故障域であるから、そういうデータになっていれば、そのうち収まるということである。⑤はワイブル分布でｍ>１となるはずで、データがそうなっていれば摩耗域となり部品交換や修理が必要になる。

9. 指数分布近似でのデータ解析による平均寿命と故障率の推定

1項の②，③，④のケースはワイブル解析から、ｍが1で故障率が指数分布であることがわかると次のような計算ができる。（ｍはちょうど1にならなくても、0.8～1.2ぐらいなら、1とみなす。）
一定時間で、観測を打ち切った場合、有意水準をα、故障数をｒ、コンポーネントアワーをＴ（総動作延時間のこと。例えば、20個を100時間観測したなら、2000時間となる。）とすると、平均寿命（MTBFともいう）の信頼区間（α=5％とした場合、この区間に95%がはいってくるという予測）の式は、故障率が指数分布の場合次のようになる。

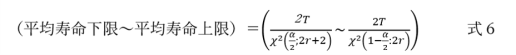
指数分布の場合、この公式が使えることに加えて、平均寿命の逆数が故障率になるので、平均寿命も故障率も信頼度もわかる。1項の②、③、④はこの公式で基本的に全て計算できる。

以上、ワイブル分布の有用性と指数分布の重要性について述べてきた。ワイブル分布は信頼性の基本でもあり、その応用の点でも有益な分布関数であるといえる。

株式会社英知継承では、本テーマに関して当該専門家による技術コンサルティング（技術支援・技術協力）が可能です。下記よりお気軽にお問い合わせください。

▼「信頼性･統計･品質工学」に関連する技術解説一覧

信頼性寿命予測の方法

故障物理からの信頼性データ解析と故障解析との違い