信頼性寿命予測の方法

寿命予測ができればこれほど便利で有益なことはない。自分の寿命が分かれば、どういう金の使い方をするか、やり残したことはなにか、いろいろと考えるであろうし手立てもたてやすい。一方、寿命が近づくにつれ不安で仕方がないし、そういうたぐいの小説もある。しかし、人間の寿命というのは、病気だけでなく、事故や災害、事件もあるから、予測不能と言ってよい。
一方、設備や機械部品・電子部品は一定条件下での使われ方が多い。使用推奨範囲や限界使用条件を定められているのが通常であるから、寿命（故障しないで機能を維持している期間、時間）が統計分布から推測できる場合が多い。
また、部品や装置の寿命が分かれば、非常に対応しやすくなる。部品の取り換え時期や、保守期間のマージン設定、定期点検頻度などが設定しやすい。5年稼働した設備があと何年もつかなど、新規設備や改造の投資計画も立てやすくなる。
ここではそれらを目的とした寿命（信頼性寿命）の考え方と基本的な計算手法を紹介する。なお、ワイブル分布や指数分布については、別稿「ワイブル分布と指数分布」にて詳細を解説する。

1. 信頼性寿命とはなにか？

信頼性寿命という専門用語自体は存在しない。信頼性工学で扱う寿命という意味である。専門用語で、寿命という言葉がかぶさるのは、特性寿命や平均寿命である。ただ「信頼寿命」という専門用語が古い本で使われている（1980年：日科技連「信頼性データの解析」）。
ここでの意味は、全体の何％が残存しているかの時間と定義されている。当解説記事でもあまり細部にこだわらず、機器や部品の機能している時間のことと広く使うことにしたい。

2. 故障との関係

信頼性と真逆にあるのが故障である。故障と信頼性は表裏一体で、どちらかを知ればよいことになる。信頼性を数値で表したものを信頼度と呼ぶが、故障については故障性や故障度という言葉はなく、故障数や故障率と呼ぶ。たいていの数理は、この故障数から故障率を算出し、そこから信頼度を求めることが多い。よって、故障数や故障率は非常に重要な信頼性寿命の元計算になる。

3. 故障率とバスタブカーブ

故障率は多くの場合、バスタブカーブと呼ばれる時間軸との関数として表現される（図1）。

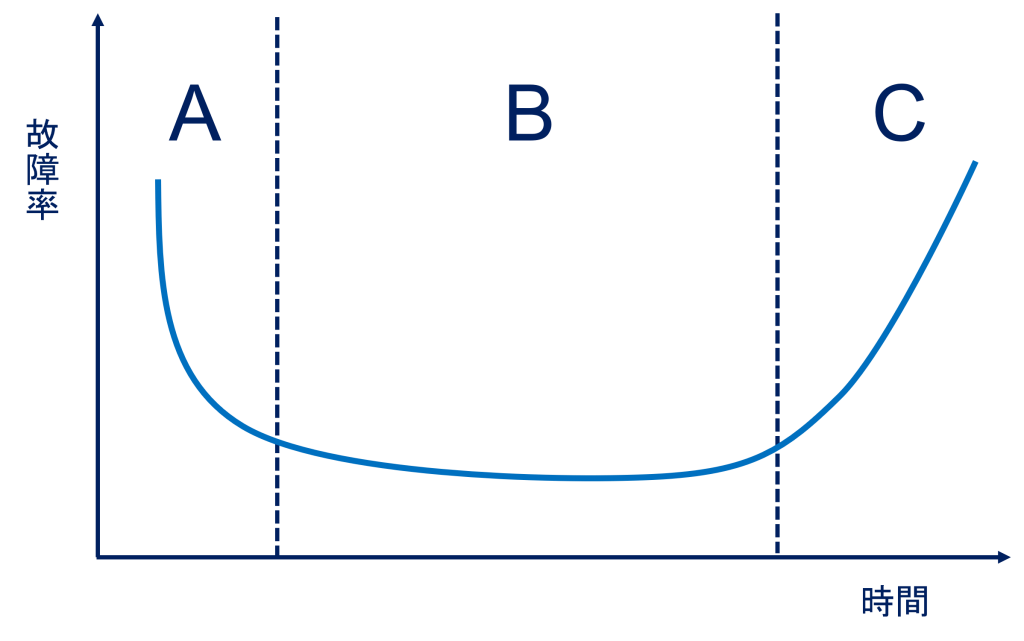
図1. バスタブカーブ

図1のバスタブカーブでは、領域Aを初期故障域、Bを偶発故障域（耐用寿命相当）、Cを摩耗故障域（寿命）と呼ぶ。それぞれの故障域によって、予測される信頼性寿命が変わってくるため、この概念は図と共に重要である。

4. A領域（初期故障）での寿命予測

初期故障域は、実際には「当たりはずれ」である。今ではめったにないが、極性間違いや異常部品組立、イモ半田による断線などのショートの類である。ヒューマンエラー、習熟度未達による低品質であっても、出荷検査にてぎりぎりで通って、使い初めに壊れるパターンがこれである。どちらかといえば、短期間に起こる事象であって、短期間で起こるから初期故障というネーミングである。このため、この期間がどのくらい続くのかについては、計算の対象にはならない。ただし、もういい加減にしてくれというのが知りたいときには、ここの予測は大事である。ワイブル分布確率紙（別記のワイブル分布を参照）を使えばすぐわかる。累積故障率をプロットし、右軸をよめば形状パラメータｍが読み取れるから、そのｍが１より小さい間は、この初期故障域だということになる。その間は、迅速な取り換えや補修が必要となる。もしくは、バーンインやエージングで逃げることであるが、最終ユーザーが実施するにはコストが犠牲となる。本来は、生産者側でこの初期故障域を小さくすることが大事である。原因にもよるが、たいていが狭義品質管理の問題であって、信頼性工学の問題としてはあまり扱われない。本稿でもこの領域に関してはこの程度での解説にとどめる。

5. B領域（偶発故障）での寿命予測

図1でもわかるように、故障率が一定（ワイブル解析では形状パラメータｍが１）である。一定なのになぜ偶発と呼ぶのかというと、初期故障のように故障率が急激に低下する方向で変化するわけではなく、次の摩耗域のように故障率が急激に上昇変化するところでもないから、その間の故障率一定期間だという解釈でよい。故障率が一定だというだけでゼロではないから、ある確率で故障は起こるがその確率は一定である。サイコロを投げて、1の目が出る確率は偶発でかつ一定との理屈と同じである。
ここでの寿命予測は非常に重要であり、信頼性工学の肝だと言ってよい。というのは、前述したように、初期故障は品質管理の問題であり、摩耗域は設計上の寿命になるので、固有技術の設計問題である。よって、この偶発故障での寿命予測は信頼性工学の重要な対象となる。また、この領域時間は耐用寿命でもある。

この領域での故障率は、その密度関数が指数分布によるものであることからきているが、実際の解析ではワイブル解析をすることが実用的である。ワイブル確率紙から、ｍ＝１の領域時間を見定め、その間は指数分布近似が使えるとして、以下の公式を使う。

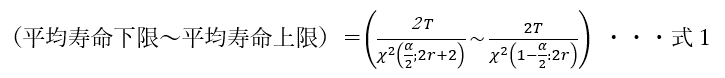
ここで、Tはコンポーネントアワー、ｒは故障した数、αは有意水準、χ2はカイ二乗分布の統計量を表す。以下に例題による解説を行う。

【例題1】 ある電子部品は20個で1000時間の間に１個故障した。この電子部品の平均寿命は、何時間と予測されるか？ 信頼水準は95％、指数分布近似にて計算せよ。

Ｔ＝20×1000＝20000時間、　ｒ＝1　信頼水準95％より、有意水準α＝5％

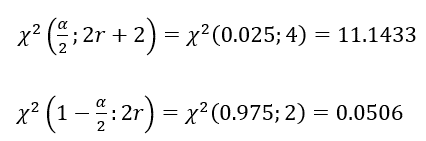
よって、平均寿命下限は、40000÷11.1433=3590 時間
　　　　平均寿命上限は、40000÷0.0506=790514時間

下限を問題にする場合が多いため、3500時間ぐらいまでがこの部品の平均寿命ということになる。ちなみに、信頼水準というのは、有意水準の反対、つまり100回試行したら95回は当たる、ということである。また、上限が790514時間であるから、いくらもっても平均で790500時間程度ということになる。この電子部品20個で、製品を構成する場合、3500時間以上は耐用寿命なので、補修か買い替えを進めることになる。ただし、790500時間以上は、摩耗域に入っているのか、いまだに偶発故障域なのかはわからない。ここまでは、あくまで偶発故障域での話であるが、それでも790500時間までの上限となる。

【例題2】 ある電子部品20個の試験で1000時間経過したが、故障数はゼロであった。この場合の平均寿命はどう推定されるか？　信頼水準は95％、指数分布近似にて計算せよ。

T＝20×1000＝20000時間、ｒ＝0　信頼水準95%より、α＝5％
故障数が観測値上ゼロのため上限はわからず無限大ともいえる。上限推定の棄却率は存在しない。存在しない分のαは下限の棄却率に入ってくるため、式１の下限は少し変わりα/2がαとなる。

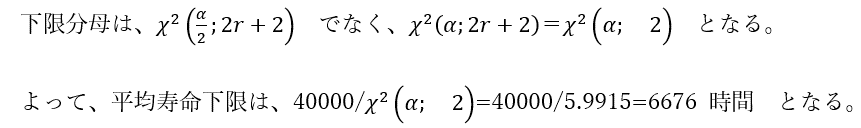
この例題から、おもしろいことがわかる。試験で故障数がゼロの場合でも、最低何時間ぐらいが平均的な寿命だと言えるかがわかるということである。20個の試験を1000時間実施し故障がゼロだといっても、7000時間はもたないということになる。たとえば、7000時間もの間、故障ゼロを保証したいシステムは不可能である。言い換えると、6600時間程度は平均寿命としては楽観できる。例題１のように1個故障した場合と比較すると大きな差である。
20個の試験あるいは使用で、1000時間経過したとき、故障数が1個の場合と0個の場合では、予測に大きな違いが出てくる。さまざまなケースにおけるリスクヘッジを考えるときに大きな助けとなる。

【例題3】 【例題2】での故障率はどう推定されるか？

故障率は平均寿命の逆数になることが分かっているため、故障率上限は0.0001497/時間、すなわち、0.015％/時間となる（故障率下限はわからない。ゼロだといいたいが大きな誤解を招く。単に今までの試験時間や試験数が足りないので、もっと試験時間を増やして故障が発生するまでみないと計算できないということである。）。
例題１においても、平均寿命の逆数をとれば故障率となる。平均寿命と故障率は逆数の関係にあるので、上限と下限も入れ替わる。言葉の問題であるが要注意である。
なお、平均寿命といっているが、故障までの平均時間MTTF（Mean time to failure）であり、平均故障間隔MTBF（Mean time between failures）でも式は同じになる。修理可能系ではMTBFを使い、非修理系ではMTTFが平均寿命の対応語となる。

6. C領域（摩耗故障域）での寿命予測

この領域での寿命予測は意味がない。すでに摩耗域に入っているからである。ただし、すでに摩耗域に入っているのかどうかを予測あるいは推定したいというのであれば、ワイブル分布による方法がよい。ワイブル確率紙を使うと、非常に簡単に平均寿命や特性寿命が推定できる。最大の特徴は、ワイブルプロットによる直線近似から、形状パラメータがはっきりすることである。形状パラメータはm値と呼ばれるが、ｍが１より小さい時には初期故障域である。ｍが１に近い時は偶発故障域であって5項のように寿命予測に指数分布が活用できる。ｍが１より大きい時には摩耗域に入っていて、この確率紙から平均寿命や特性寿命が推定される。ただし、推定であって本来の予測ではない。
ただ、この領域におけるｍ値は重要である。たとえば、加速試験を設計するとき、加速係数のみを考えるのではなく、加速度合いが2倍、3倍になったとしても、実際の信頼性試験での形状パラメータｍが一致しなければ意味がない。形状パラメータが一致しないということは、劣化モード、メカニズムが違うということになるから、加速試験とは言えない。たとえば、形状パラメータｍが大きく変化して、ｍが3から５になったとしたら、全く別のメカニズムで壊れていることになる。
ワイブル確率紙でいえば、傾きが変わらないことが重要である。これが変わった場合には、加速試験とは言えない。破壊試験になっている恐れもある。そういう意味での予測は可能かつ重要である。言い換えると、形状パラメータが等しい加速試験であるならば、実使用状態での寿命予測が可能となる（加速係数倍すればよいことになる）。

以上、寿命予測について述べたが、非常に基本的な手法について紹介している。応用的な方法もまだいくつかあるが、機会あれば紹介したい。

株式会社英知継承では、本テーマに関して当該専門家による技術コンサルティング（技術支援・技術協力）が可能です。下記よりお気軽にお問い合わせください。

▼「信頼性･統計･品質工学」に関連する技術解説一覧

ワイブル分布と指数分布

故障物理からの信頼性データ解析と故障解析との違い